Подробное решение Задания № 5 «Проверьте себя» в тестовой форме для учащихся 8 класса, учебник Алгебра, авторы Мерзляк, Полонский, Якир.
Задание № 5 «Проверьте себя» в тестовой форме
1. Какое из данных уравнений не является квадратным?
А) x2 = 0
Б) x2 + х = 0
В) x3 + x = 0
Г) x2 + x — 2 = 0
2. Решите уравнение 9x — x2 = 0.
А) -3; 0; 3
Б) 0; 3
В) -3; 3
Г) 0; 9
3. Решите уравнение (x2-x)/6 — (x — 2)/3 = (3 — х)/2.
А) 0; 5
Б) 5
В) корень 5
Г) -корень 5; корень 5
4. Какое изданных уравнений не имеет корней?
А) x2 — 5x — 2 = 0
Б) x2 — 5x + 2 = 0
В) x2 — 2x + 5 = 0
Г) x2 + 2x — 5 = 0
5. Сколько корней имеет уравнение 6x2 + 13x + 5 = 0?
А) два
Б) бесконечно много
В) ни одного
Г) один
6. Найдите корни уравнения x2 + 4x — 21 = 0.
А) 7; -3
Б) -7; 3
В) -7; -3
Г) 3; 7
7. Чему равна сумма корней уравнения x2 — 10x — 12 = 0?
А) 10
Б) -10
В) -12
Г) 12
8. Чему равно произведение корней уравнения Зx2 — 16x + 6 = 0?
А) 6
Б) 2
В) -16
Г) 16/3
9. При каких значениях переменной принимают равные значения выражения (Зx — 1)(x + 2) и (x — 12)(x — 4)?
А) -12,5; 2
Б) 12,5; -2
В) -25; 4
Г) 25; -4
10. Составьте квадратное уравнение, корни которого равны 3 — корень 2 и 3 + корень 2.
А) x2 + 6х — 7 = 0
Б) x2 — 6x — 7 = 0
В) x2 + 6x + 7 = 0
Г) x2 — 6x + 7 = 0
11. Решите уравнение x|x| — 9x — 10 = 0.
А) — 1; 10;
Б) 10;
В) -1;
Г) -1; 10
12. Число -5 является корнем уравнения 2x2 + 9x + с = 0. Найдите второй корень уравнения и значение с.
А) x2 = 0,5, с = -5
Б) x2 = -0,5, с = 5
В) x2 = 9,5, с = 22,5
Г) x2 = 9,5, с = -22,5
Ответ:

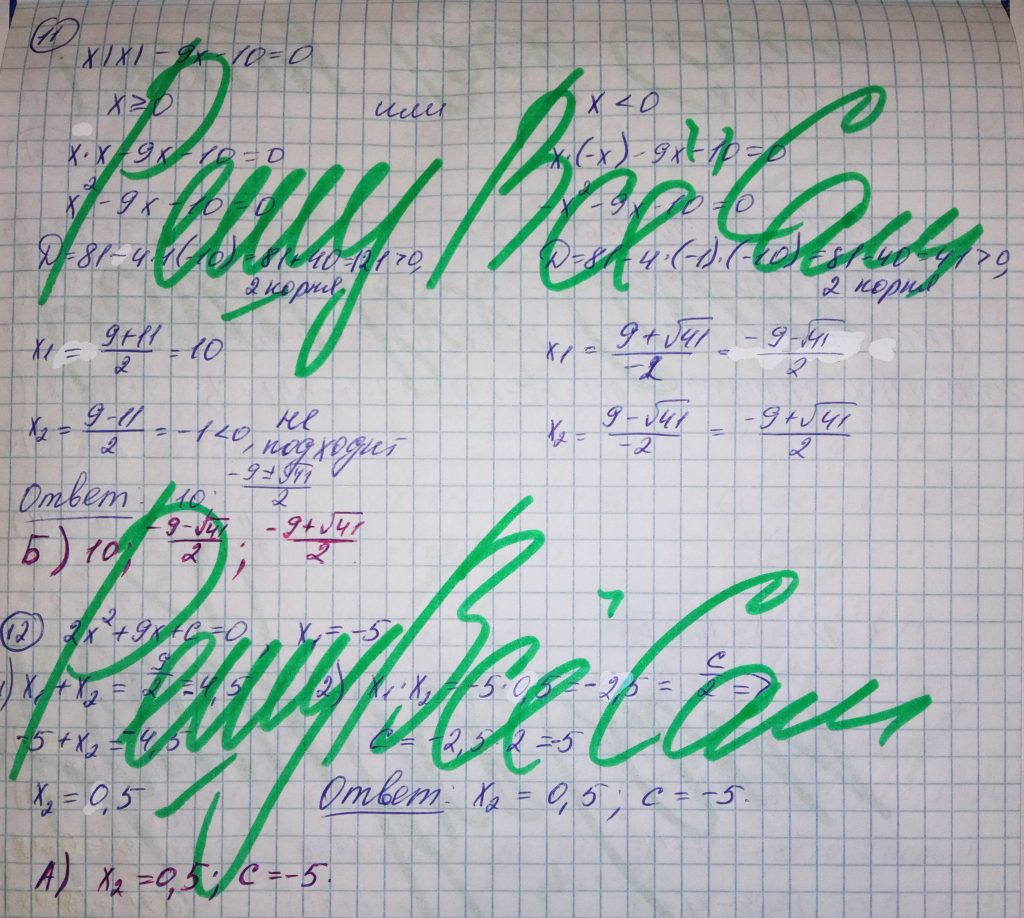
22. Квадратный трёхчлен
